Métrologie du Coricancha : Pérou, Cusco Quentin LEPLAT
- Auteur/autrice de la publication :Fehmi Krasniqi
- Publication publiée :10 mars 2024
- Post category:News/Publications Fehmi Krasniqi
Métrologie du Coricancha : Pérou, Cusco
Métrologie historique 1 sur 17 Coricancha
Quentin LEPLAT

quentin.leplat@protonmail.com
Septembre 2018
Métrologie du Coricancha : Pérou, Cusco
Résumé : Lors d’un séjour au Pérou, je pris le temps de mesurer avec un télémètre les deux salles du célèbre temple Pré-inca du Coricancha à Cusco. Les dimensions de ce monument révèlent une géométrie subtile et la connaissance du nombre d’or, exprimée à travers cette géométrie ainsi qu’à travers les nombres. De surcroît, ce temple révèle l’emploi d’unités de mesure anachroniques, puisque le mètre et le yard mégalithique sont les deux principales unités de mesure ayant servi à l’organisation géométrique du Coricancha. Leur utilisation est d’une telle évidence que ce constat bouscule radicale ment nos croyances quant à l’origine des civilisations d’Amérique du Sud.
Outre ces deux mesures, on constate que la coudée royale égyptienne et la coudée ni lométrique font aussi partie des unités de mesure employées. Toute la construction ré vèlent de manière simple et limpide l’emploi d’unités de mesure à priori sans aucun rap port entre elles, et très éloignées dans l’espace et le temps.
Les dimensions des salles du Coricancha sont une révolution pour notre vision classique de l’Histoire des premières grandes civilisations, car elles démontrent que des relations scientifiques ont existé entre l’ancien et le nouveau monde il y a plusieurs millénaires, par un peuple inconnu.
Mots-clefs : pré-inca, Pérou, Coricancha, Cusco, métrologie, yard mégalithique, mètre, coudée royale, nombre d’or.
Métrologie historique 2 sur 17 Coricancha
Les dimensions de la grande salle : enceintes A et B
Le plan ci-dessous (Figure 1) indique en noir les constructions pré-incas encore vi 1 – sibles. Nous allons nous intéresser aux deux salles qui sont encore complètes et que tout le monde peut visiter. Nous ne nous attarderons pas sur la finesse technique de l’ouvrage, qui suscite pourtant l’admiration de tous les observateurs.
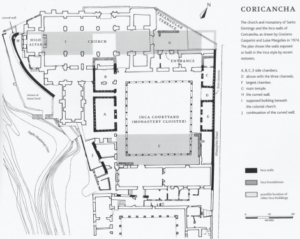
Figure 1 : plan du Coricancha
Les salles A et E sont celles que nous avons étudiées et dont il est possible de connaître les dimensions intérieures, extérieures ainsi que l’épaisseur des murs avec un télémètre de chantier Leica Disto 810.
Graziano Gasparini and Luise Margolies in 1974 1
Métrologie historique 3 sur 17 Coricancha
La salle A (ci-dessous) de forme rectangulaire était autrefois séparée par un couloir que  l’on aperçoit encore, d’une autre salle identique. Ces salles comporte des niches que l’on aperçoit très bien sur cette photo.
l’on aperçoit encore, d’une autre salle identique. Ces salles comporte des niches que l’on aperçoit très bien sur cette photo.
Cette salle mesure sur son plan au sol intérieur : 12,945 ± 0,005 m par 8,035 ± 0,005. Métrologie historique 4 sur 17 Coricancha
L’épaisseur des murs est de 1,00 m ± 0,005 (photo ci-contre). Les dimensions extérieures sont de 10,001 ± 0,005 m par 14,889 ± 0,005 m. Les deux murs latéraux étant un peu moins épais que les murs de façade (0,972 m par calcul). Nous allons voir que cette différence a une fonction géométrique, métrologique et numérique très importante. Il ne s’agit aucunement d’une erreur de conception ou d’une ap proximation des bâtisseurs.
Premier constat évident : la largeur semble calibrée en mètres, puisqu’elle mesure 10 m. L’épaisseur des murs vient confirmer cette mesure métrique, puisque l’on retrouve 1 m pour l’épaisseur du mur de façade (voir photo précédente). La largeur intérieure me sure donc 8 m. Toutefois, la base des murs du Coricancha est sensiblement rentrante vers l’intérieur, si bien que la mesure délivre une mesure de 8m035, alors que le calcul à partir de la mesure extérieure (10,001 m ± 0,005) que nous avons mesuré au niveau des fondations, moins l’épaisseur des murs de (1,004 m ± 0,05) donne en théorie une mesure de 8 m ± 0,05. Il se peut que le niveau du sol intérieur de l’enceinte fût sensi
blement plus haut à l’époque de sa construction. Nous pouvons estimer la largeur inté rieure à 8,014 m ± 0,021.
Deuxième constat simple : le rapport de proportion entre la largeur et la longueur de la salle à l’intérieure est un rapport « doré » :

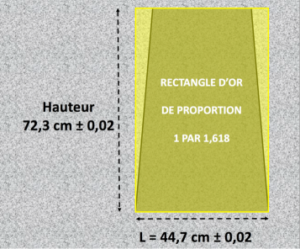
En effet, ce rapport de proportion est celui du nombre d’or. On retrouve ce rapport dans les niches qui se trouvent dans l’autre salle (E sur le plan) puisque celle-ci mesure 72,3 cm ± 0,2 par 44,7 cm ± 0,2, soit un rapport de 1,61744 (Figure 2).
Métrologie historique 5 sur 17 Coricancha
Figure 2 : schéma des dimensions des niches dans la salle E du Coricanch
Métrologie historique 6 sur 17 Coricancha . Le tracé géométrique du nombre d’or à partir d’un carré de 44,72 cm : ![]()
 La présence du nombre d’or peut se réaliser avec un tracé géométrique, avec comme point de départ un carré (ici de 44,72 cm). Mais ce qui est intéressant, c’est que la dia gonale d’un double carré est de 100 cm. Cette relation géométrique entre une coudée de 44,72 cm et 1 mètre montre que cette mesure de 44,72 cm est liée à la mesure mé trique.
La présence du nombre d’or peut se réaliser avec un tracé géométrique, avec comme point de départ un carré (ici de 44,72 cm). Mais ce qui est intéressant, c’est que la dia gonale d’un double carré est de 100 cm. Cette relation géométrique entre une coudée de 44,72 cm et 1 mètre montre que cette mesure de 44,72 cm est liée à la mesure mé trique.
Intéressons-nous aux dimensions extérieures de la salle principale. Nous avons vu que celle-ci mesure 10 m par 14,89 m. Soit un périmètre de 49,78 m. Cette mesure du pé rimètre vaut exactement 60 yards mégalithiques de 82,944 cm.
Ce constat est étonnant, d’autant plus que les niches de cette salle mesurent 82,9 cm ± 0,03 (Figure 3).
Métrologie historique 7 sur 17 Coricancha
Figure 3 : niches de la salle A du Coricancha
Le yard mégalithique est la plus ancienne unité de mesure dont nous ayons retrouvé la trace. Son existence remonte à une époque où les humains érigèrent les menhirs et les dolmens, soit 4500 ans (environ) avant notre ère. Cette unité de mesure fut trouvée par le professeur Alexander Thom de manière statistique, dans un premier temps en 2 mesurant des centaines de cercles de pierre, puis dans un second temps sur de plus longues distances entre des monuments mégalithiques majeurs, ces dernières années.
Retrouvée de l’autre coté de l’océan Atlantique, cette mesure pose un sérieux problème à notre vision de l’Histoire. Ou bien il s’agit d’une pure coïncidence, ou bien cette me sure s’est répandue par l’intermédiaire d’un peuple inconnu jusqu’au cœur des plus grandes civilisations d’Amérique du Sud.
THOM A : 1955. A Statistical Examination of the Megalithic Sites in Britain. Source : Journal of the Royal 2 Statistical Society. Series A (General), Vol. 118, No. 3 (1955), pp. 275-295. Published by Wiley for the Royal Statistical Society. Stable URL : http://www.jstor.org/stable/2342494
Métrologie historique 8 sur 17 Coricancha
Il convient de rappeler que le métrologiste historique Rottlander 3 4 a notamment démon tré que le yard mégalithique (qui existe aussi sous la forme d’une toise de 2,5 yards de 2,0736 m) a donné naissance à la coudée de Nippur 2500 ans plus tard, et à plusieurs milliers de km du lieu où le Yard mégalithique fut observé au préalable il y a 7000 ans en Europe de l’ouest. En effet, 4 coudées de Nippur mesurent exactement un yard mégali thique.
Il y a donc un lien entre la connaissance des peuples mégalithiques de l’Europe de l’Ouest et les Sumériens. Ce lien peut également être constaté par le fait que l’autre coudée sumérienne connue à ce jour, qu’on appelle « coudée de Gudéa », est liée à la coudée de Nippur.
L’on constate dès lors que le périmètre de l’enceinte A du Coricancha vaut exac tement 100 coudées sumériennes de Gudéa ou 60 yards mégalithiques.
En plus de trouver le mètre comme unité de mesure, on y retrouve les mesures mégali thiques qui se sont exportées jusqu’en pays de Sumer entre -5000 et -3000 ans avant notre ère.
La présence simple de ces deux unités de mesure, liées au nombre d’or, rend le hasard très peu probable… nous pouvons affirmer que le hasard n’a rien à voir avec ces obser vations métrologiques, et cela d’autant plus que le périmètre intérieur de l’enceinte dé
ROTTLANDER R.C.A : 1999. Measurment units of the linear pottery culture and ancient metrology. 3 Archäologisches Korrenzpondensblatt, 1999, vol. 29, N°2, p. 189-20
ROTTLANDER R.C.A : 1979, « Antike Längenmasse », Braunschweig/Wiesbaden (DE), Friedr. Vieweg 4 & Sohn.
Métrologie historique 9 sur 17 Coricancha
livre une autre mesure antique, existant il y au moins 4500 ans de l’autre coté de l’océan Atlantique.
En effet, le périmètre intérieur de l’enceinte A du Coricancha est de 41,88 m ± 0,05, soit 80 coudées royales égyptiennes de 0,5236 cm ± 0,0003.
Dire que la coudée royale est employée ici est une hérésie au regard des consensus en matière de diffusion des connaissances depuis l’Antiquité ! Et pourtant, si l’on mesure la distance des deux salles identiques qui sont côte à côte et séparées par un couloir de 1,618 mètres, la longueur totale est de 60 coudées royales à 0,05% de précision (voir Figure 4).
Figure 4 : maquette du Coricancha avec les deux
salles identiques séparées par un couloir de
161,8 cm
La largeur du couloir est de 1,618 m ± 0,03 : ce nombre est tout simplement l’expression du nombre d’or en unité métrique. Autre curiosité la longueur totale de 60 coudées égyptiennes vaut 10 fois le nombre PI en mètre également.
Mais ce n’est pas tout, puisque la longueur intérieure de 12,945 m ± 0,001 mesure exac tement 24 unités d’une autre mesure égyptienne. Il s’agit de la coudée nilométrique, dé couverte pour la première fois par les savants français5 de l’expédition d’Égypte de Na poléon. Cette coudée mesure 53,93 ± 0,01 cm, est celle qui fut employée pour bâtir la
EDME- FRANÇOIS JOMARD… ET AL. 1822, Description de l’Égypte ou Recueil des observations et 5 des recherches qui ont été faites en Égypte pendant l’expédition de l’armée française. Tome 7, page 7 ; page 167-169
Métrologie historique 10 sur 17 Coricancha
pyramide de Khéphren, qui mesure à la base 400 de ces coudées . J’ai expliqué déjà 6 que la coudée nilométrique vaut 1/3 du nombre d’or exprimé en mètres, et que c’est jus tement ce qui relie ces deux mesures à travers des nombres que les égyptiens manipu laient avec aisance, dans l’espace et le temps. La présence d’un couloir de 1,618 m entre les deux grandes enceintes est une façon de plus d’indiquer l’emploi du mètre, et cela confirme encore la connaissance de la coudée nilométrique.
Cela amène un autre constat métrologique et symbolique en relation avec le nombre d’or :
Résumons-nous : les dimensions et périmètres intérieurs et extérieurs de l’en ceinte A se mesurent au moyen d’au moins quatre unités :
Le mètre (largeur intérieure et extérieure, et épaisseur du mur de façade)
Le yard mégalithique et la coudée de Gudéa (périmètre extérieur et hauteur des niches)
La coudée royale égyptienne (périmètre intérieur et longueur totale des deux en ceintes)
La coudée nilométrique de Khephren (longueur intérieure et largeur du couloir)
Il est impossible que ces mesures, qui sont les mesures les plus anciennes connues à ce jour par les historiens métrologistes, soient présentes par hasard sur un temple majeur de l’art pré-inca. La probabilité qu’une simulation, réalisée au hasard d’un temple, dispose de caractéristiques du même ordre, est si infime que le doute n’est pas permis quant à la diffusion de ces très anciennes mesures de l’autre coté de l’océan Atlantique.
La finesse métrologique ne s’arrête pas là. En effet, nous l’avons vu, la longueur exté rieure mesure 14,89 m ± 0,005 soit, exprimée en yard mégalithique : 17,94 ym ± 0,1. Or, la diagonale de l’enceinte mesure 17,94 ± 0,1. Il s’agit d’un jeu numérique qui interpelle,
LEPLAT QUENTIN : 2017, La coudée nilométrique de la pyramide de Khéphren et le mètre. http:// 6 messagedelanuitdestemps.org/wp-content/uploads/2017/10/La-coudée -nilométrique-de-Khéphren.pdf
Métrologie historique 11 sur 17 Coricancha
car cela signifie que le rapport de proportions entre le mètre et le yard mégalithique est le même qu’entre la longueur de l’enceinte et sa diagonale (voir plan ci-dessous)
Selon le même type de principes, nous avons dans cette salle des niches de deux di mensions différentes. Celle de la façade de l’entrée mesure 44,7 cm ± 0,1 par 82,9 cm ± 0,1. Or ce rapport est le même qu’entre le mètre et la coudée nilométrique de Khephren.
Métrologie historique 12 sur 17 Coricancha
Là encore, cet indice dévoile clairement la connaissance des rapports de proportions entre les différentes unités de mesure employées. Nous pouvons même proposer un autre rapport de proportions entre la longueur extérieure de 14,89 mètres et la largeur intérieure que nous avons mesurée à 8,03 et dont on se demande si le fait qu’il y ait une déformation du mur à la base ne permet pas justement d’exprimer le rapport entre le mètre et la coudée nilométrique.
Regardons les dimensions des autres niches. Elles sont un peu plus larges à la base car elles mesurent 47,9 ± 0,2 cm au lieu de 44,7 cm. La hauteur mesure 82,9 cm, soit un yard mégalithique. Si bien que le rapport hauteur/largeur est de 1 sur 1,732, c’est-à dire la racine de 3.
Métrologie historique 13 sur 17 Coricancha La seconde salle du Coricancha : salle E
La seconde salle encore complète que l’on peut visiter est intéressante aussi. En effet, elle mesure 4,15 m ± 0,02 par 11,62 m ± 0,02 et l’épaisseur des murs est de 0,829 ± 0,03 m. Ce qui veut dire que l’intérieur de cette enceinte mesure 5 par 14 yards mégali thiques et que l’épaisseur des murs, comme dans l’autre salle, indique l’unité de mesure employée, en l’occurence le yard mégalithique.
Ce qui est intéressant, c’est que comme avec l’autre salle, l’épaisseur du mur est une indication qui nous aide à découvrir l’une des unités de mesure employées.
Intéressons-nous aux niches de cette salle qui, nous l’avons vu en début d’article, me surent 72,3 cm par 44,7 cm de large, soit le ratio du nombre d’or.
Métrologie historique 14 sur 17 Coricancha
La mesure de 44,7 cm est pour moi un emploi de l’unité métrique. En effet, 44,72 cm c’est 20 fois la racine de 5 (20×2,236 = 44,72). Cette mesure est employée à Tiwanaku, comme nous l’avons démontré dans une récente publication. Cette unité de mesure est 7 fondamentale au Pérou, en Bolivie, mais aussi sur le site de Teotihuacan par exemple, puisque l’allée des morts mesure, depuis la face nord de la Pyramide de la Lune jusqu’à la face sud du temple de Quetzalcoatl, 2236 mètres, soit 5000 coudées de 44,72 cm. Quant au périmètre de la base de la Pyramide du Soleil, il mesure 894 m, soit 2000 coudées de 44,72 cm.
La mesure 72,3 cm est importante aussi, car son carré délivre la valeur de la coudée royale égyptienne. En effet, 7,236 x 7,236 = 52,36.
Une étude plus approfondie des dimensions de ces niches révèle un système métrolo gique d’une extrême subtilité, mettant de nouveau en évidence l’emploi des mesures mégalithiques et du mètre.
LEPLAT Quentin, Septembre 2018, Étude et observation métrologique à Tiwanaku en Bolivie 7
Métrologie historique 15 sur 17 Coricancha
Le pied de Nippur est en fait un pied mégalithique, puisque ce dernier vaut 1/3 de yard (27,64 cm).
Le plan des niches (Figure 5) se passe de commentaires, tout esprit cartésien et sans parti pris reconnaîtra l’évidente subtilité de la science « géo-métrologique » de ces an ciens bâtisseurs de génie, qui marièrent les mesures et les proportions avec une éton nante simplicité.
La géométrie et les dimensions de ces niches indiquent au minimum l’emploi d’une pro portion liée au nombre d’or ainsi que l’usage des mesures mégalithiques et du mètre moderne. Quant au mètre, si vous en doutez encore, notez que la surface de la niche est de 3000 cm2 (72,36 x 41,47 ≈ 3000 cm ± 0,025%. Et puis, si l’on se penche simple ment sur le tracé géométrique qui permet d’obtenir ce rapport hauteur/largeur, on constate qu’il est conçu avec un carré de base de 44,72 et qu’il faut rajouter 50 cm pour obtenir la hauteur de la niche.
Le yard mégalithique sur de longues distances :
Je ne résiste pas à vous montrer que cette mesure mégalithique fut employée sur de très longues distances par les bâtisseurs de ces grandes cités et temples pré-incas, exactement comme le faisaient les peuples mégalithiques. En effet, la ligne virtuelle entre le monolithe de la place centrale du Machu Picchu détermine un angle de 31,72° avec le monolithe de Quenko juste au-dessus de la cité de Cusco. Cette ligne
Figure 5 : niche de la salle E du Coricancha
Métrologie historique 16 sur 17 Coricancha
mesure, d’après Google Earth, 73140 m, en tenant compte de la différence d’altitude entre ces deux lieux.
L’angle de 31,72° est celui de la diagonale d’un rectangle de proportion 1 par 1,618, c’est-à-dire un rectangle d’or. Cet azimut est très précis puisqu’il est déterminé à partir de deux monolithes majeurs et exceptionnels au Machu Picchu et dans les environs de Quenko. La distance de la diagonale de ce rectangle d’or mesure exactement 30 000 toises mégalithiques sur le côté Est-Ouest. 8
Non seulement le yard mégalithique est employé sur les monuments, mais il est aussi employé sur de très longues distances, comme le faisaient les bâtisseurs de méga lithes en Europe ou les bâtisseurs des grandes pyramides en Égypte . 9 10
8 La toise mégalithique mesure 2,5 yards mégalithiques, c’est-à-dire 2,0736 m. Cette mesure est em ployée avec le yard mégalithique sur de nombreux sites mégalithiques et sur de longues distances éga lement.
CROWHURST Howard 2016, Le plan des Pyramides, de Carnac en Bretagne jusqu’à Karnak en 9 Égypte. Éditions Epistemea.
LEPLAT Quentin 2018 : Étude statistique et méthodique des stratégies d’arpentage géométrique en 10 Égypte et la connaissance des dimensions de la Terre.
Métrologie historique 17 sur 17 Coricancha
Conclusion :
Cette étude métrologique démontre que le yard mégalithique fut employé dans la conception du temple du Coricancha au Pérou. Cette unité de mesure n’est pas la seule, puisque l’on détecte assez simplement la coudée royale égyptienne, la coudée de Gudéa et la coudée nilométrique. Mais le plus surprenant reste que le mètre est em
ployé aussi dans ce monument majeur de l’architecture pré-inca. L’unité métrique est employée sous sa forme brute de 1 m, ou sous la forme d’une coudée de 44,72 cm. Tout cela suppose la connaissance de la mesure de la Terre. Chose possible, puisque pour ce faire il faut maîtriser les méthodes de triangulation et les exécuter sur de longues distances, comme le prouve le lien géométrique et métrologique entre le mono
lithe du Machu Picchu et le monolithe de Quenko.
Ces constats métrologiques bousculent radicalement l’idée que nous nous faisons de la diffusions des connaissances scientifiques de nos ancêtres et de leurs échanges cultu rels. Il n’est possible d’en comprendre le sens qu’en intégrant un autre mode de pensée où les nombres ont une importance fondamentale, car ils sont les bases d’un langage universel que seule la mesure est à même de révéler.






